백준 11947번: 이런 반전이 (C++)
2023. 1. 20. 19:12ㆍ알고리즘/수학

https://www.acmicpc.net/problem/11947
11947번: 이런 반전이
첫째 줄에는 테스트 케이스의 개수를 나타내는 하나의 자연수 T가 주어집니다. 다음 T개의 각 줄에는 하나의 양의 정수 N이 주어집니다. (1 ≤ N ≤ 1,000,000,000)
www.acmicpc.net
풀이
처음에 문자열로 1부터 하나씩 계산해보려다가 n이 최대 10억이라서 시간초과가 난다고 생각이 들었다.
그래서 고등학교때 배웠던 함수의 최댓값을 활용했다.
우선, 정수 n을 4자리 수 abcd의 형태로 나타내고 식을 세워보았다.


이렇게 n과 F(n) 을 곱한다고 가정했을 때, 초항이 큰 수가 최댓값이 된다는 것을 알았고
a에 대한 2차원 함수를 그려보니
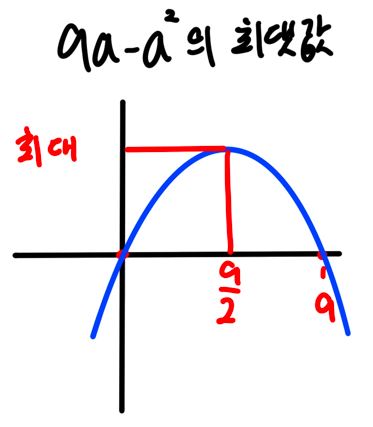
a가 4.5일 때, 최댓값이 된다. a는 정수이기 때문에 4 or 5 가 된다.
502 * 497 = 249,494
501 * 498 = 249,498
500 * 499 = 249,500
499 * 500 = 249,500
498 * 501 = 249,498
497 * 502 = 249,494
.
.
.
실제로 값을 계산해보니 499... * 500... 꼴이 가장 크고 숫자가 더 커지면 작아진다.
그래서 앞자리가 5이상이면 499... * 500... 꼴로 계산을 해주었고
앞자리가 5보다 작다면 a * (9 - a) * 10 ^ i 으로 F(n)을 구해서 n을 다시 숫자로 변환시켜서 사랑스러움을 구해주었다.
전체 코드
#include <iostream>
#include <cmath>
#include <string>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int T;
cin >> T;
while (T--) {
string N;
cin >> N;
long long love = 0;
if (N[0] >= '5') {
love = 5 * pow(10, N.size() - 1) * (5 * pow(10, N.size() - 1) - 1);
}
else {
for (int i = 0; i < N.size(); i++) {
love += (9 - ((long long)N[i] - '0')) * pow(10, N.size() - i - 1);
}
love *= stoi(N);
}
cout << love << '\n';
}
}'알고리즘 > 수학' 카테고리의 다른 글
| 백준 2502번: 떡 먹는 호랑이 (C++) (0) | 2023.01.18 |
|---|---|
| 백준 1111번: IQ Test (C++) (0) | 2023.01.18 |
